
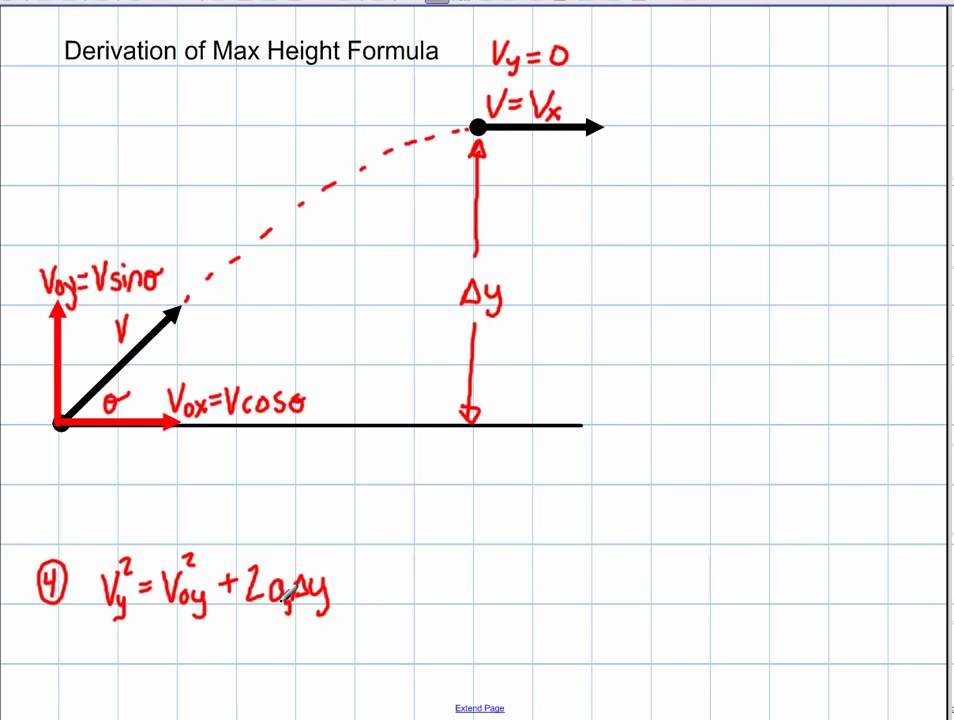
The launch velocity of a projectile can be calculated from the range if the. Should I say that since there is this wind, then the initial velocity of the projectile will be the same as the one of the wind? Or how should I do it? Position and speed at any time can be calculated from the motion equations. I was thinking of a projectile of mass $m$, launched at a $\textit$. Horizontal motion: The horizontal motion is not accelerated. In component form, the above equation becomes (176) (177) Here, is the terminal velocity: i.e. Vertical motion: Gravity produces accelerated motion of the projectile. First of all the $z$ axis points upwards, the $x$ axis is horizontal, positive to the right and therefore $y$ where is the projectile velocity, the acceleration due to gravity, and a positive constant. The magnitudes of the displacement s along x- and y-axes are called x and y.

These axes are perpendicular, so A x A cos and A y A sin are used. But in fact air resistance (often called air drag.
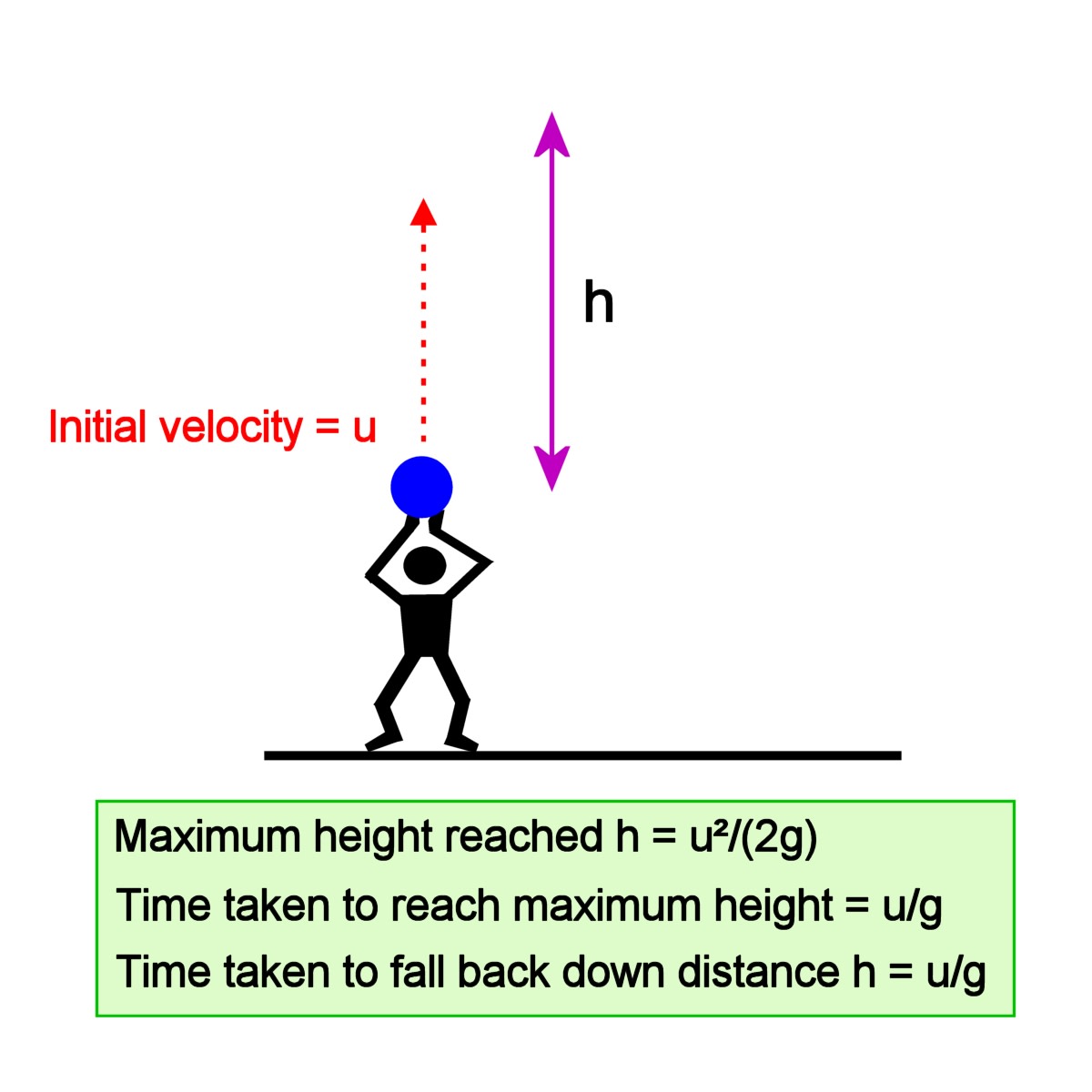
However my problem is way simpler than that. The following steps are used to analyze projectile motion: Separate the motion into horizontal and vertical components along the x- and y-axes. In our study of projectile motion, we assumed that air-resistance effects are negli- gibly small. Derive the equations of motion (hence of velocity and acceleration too) in each coordinate for the following problem.įirst of all, this question is very similar (in a sense) to this one Projectile Motion with Air Resistance and Wind.


 0 kommentar(er)
0 kommentar(er)
